方形と正方形の面積) B① C① D② 展 4 長方形や正方形の面積の公式を使えるように 複合図形を補助線で分けたり、図形を補ったりし て、面積の求め方を考える。 ・複合図形の面積の多様な求め方を理解すること。 (本時) 平行四辺形の面積は、 「面積 底辺 高さ」 「 面 積 = 底 辺 × 高 さ 」 で求められます。 たとえば、「底辺 4 c m ,高さ 3 c m の平行四辺形」の面積は 4 × 3 = 12 c m 2 となります。 これは、平行四辺形の右端の直角三角形を切り取って左側に移すと 「たて 3 c m正方形面積はいくつ? 課題1 正方形の面積はそれぞれ何㎠ですか。 ① ㎠ ② ㎠ ③ ㎠ ④ ㎠ ⑤ ㎠ ⑥ ㎠ ⑦ ㎠ ⑧ ㎠ ⑨ ㎠ 青の正方形と赤の正方形の違いは何ですか? 無理数 氏名 №2

正方形面積題目newasiabooks Com Xirafs
正方形面積
正方形面積-台形の1辺・面積(3辺の長さと高さから) ひし形の面積 平行四辺形の面積(底辺と高さから) 平行四辺形の面積(2辺と夾角から) 円に内接する四角形の面積(4辺から) 四角形の面積(4辺と対角の和から) 正多角形の面積 正多角形の面積から辺 円の面積正方形是特殊的平行四边形,也是特殊的长方形。在同一平面内:四条边都相等且一个角是直角的四边形是正方形 3 。 有一组邻边相等的矩形是正方形。 有一个角为直角的菱形是正方形。 正方形对角线相等




求正方形的面积 Youtube
正方形abcdと正方形efghの面積比が32でa=1のときbの値を求めなさい この問題の解法を誰か教えてください 数学 面積が1haの正方形の形をした広場に面積が1m2の正方形の形をした人工芝を敷き詰めるには、芝が何枚必要ですか?・1㎡,1a,1ha,1㎢の正方形 の1辺の長さと面積の関係を調べ る。 10 ・面積の単位と測定 の意味,長方形や正 方形の面積の公式 を理解している。 ・面積の単位の関係 を理解している。 ・学校の校舎を上空から 見取った複合図形につい 正多角形の面積の公式 1辺の長さを a ~a~ a とした、正三角形から正六角形までの面積を求めます。 Ⅰ 面積の公式 Ⅱ 面積の公式の証明 Ⅰ 面積の公式 1辺 a ~a~ a の正四角形(正方形) と求まる。 三角比の値が、手計算でわかる n ~n~ n の値は、 n = 3, 4
(正方形abcd) = (対角線ac)×(対角線bd)÷2 = 10×10÷2 = 50 cm^2 になるよ。 計算ミスしないように、ゆっくり解いてみてね! まとめ: 正方形の面積の求め方の公式は2つで十分! 正方形の面積の求め方は2つ。 正方形の、 辺の長さ;4年算数 大きい面積の求め方 子どもの学習支援 by いっちに算数 スマホ版 前のページに戻る 教え方4 平方メートル の単位を教え、平方メートル と平方センチメートル の単位の関係に気づかせます。 そのあとで、㎝とmの単位を混合した正方形や長方形の面積を求める問題を考えさせます。(2)每个面的面积等于边长乘以边长,每个面都是正方形,设边长为a,则面积为a×a=a²。 (3)六个面的面积之和为a²×6=6a²。 扩展资料: 正方体的特征: 〔1〕正方体有8个顶点,每个顶点连接三条棱。 〔2〕正方体有12条棱,每条棱长度相等。
正方形の面積を求める2つの公式 具体例で学ぶ数学 > 図形 > 正方形の面積を求める2つの公式 最終更新日 ~公式その1~ 1辺の長さが分かっている正方形の面積は (1辺)× (1辺) または (たて)× (よこ) で求めることができる。 ~公式その2~ 1cm方眼を利用して面積が3,6,7平方センチメートルの正方形の作り方を教えてください!!コンパスを使っていいなら簡単で, いずれも「その正方形の辺の長さをどのように求めるか」という勝負になります1 3cm^2 の場合1 直径が (31)=三角形 (さんかくけい) の 面積 (めんせき) の求め方の 基本 (きほん) は「 底辺 (ていへん) × 高 (たか) さ ÷ 2」ですが、高さが分からないときに 他 (た) の 情報 (じょうほう) から面積を求める 公式 (こうしき) がいくつもあります。 ここでは、三辺の長さが分かっている 場合 (ばあい) や、 角度



长方形与正方形面积计算 二 面积计算 奥数网



小学几何数学 两正方形面积相差145 求大正方形面积 网易视频
正方形の面積が分かっているとき、辺の長さは簡単に求められます。 a=√A です。正方形の面積がA=a^2なので、ルートをとれば1辺の長さが逆算できます。 まとめ 今回は正方形の面積について説明しました。簡単な公式で計算できます。三平方の定理の証明|直感的に分かる図で解説します 管理人 5月 23, / 5月 27, 三平方の定理は直角三角形の辺の長さに関する定理ですが、今後、図形だけではなく関数などあらゆる分野でも利用することになる重要な定理です。 今回は三平方の定理中学受験算数問題(円の面積)中学受験算数問題(ヒポクラテスの三日月)中学受験算数(正方形の回転)木の葉形の面積(1997 灘中 改題)木の葉形面積(灘中1998 類題)平面図形の面積(灘 07)正五角形の面積(東海 04)正三角形と正六角形




己知正方形面积求边长的方法 百度经验




用部分单位正方形测量面积 视频 面积和面积单位 可汗学院
三角形の面積 ・正三角形の面積 1辺の長さを指定して、正三角形の面積を計算します。 ・三角形の面積(底辺と高さ) 底辺と高さから三角形の面積を計算します。 ・三角形の面積(2辺と間の角度) 2辺と間の角度から三角形の面積を計算します。正八角形の対角線で囲まれた面積 東海中 08 円内を転がる正方形 雙葉中 07・6 転がる正方形 清真学園中 06・後期・3 長方形の通過する部分の面積など ラ・サール中 11・5 辺の通過する部分の面積 灘中三角形の面積は「 \(底辺×高さ÷2\) 」という公式から求まりますが、この公式以外にも色々な方法で三角形の面積を求めることができます。 このページでは、そんな三角形の面積の求め方をタイプ別に見ていきましょう。




一个正方形的边长是奇数它的面积一定是 小学四年级下学期数学




正方形面積題目newasiabooks Com Xirafs
6年算数 円の面積1 子どもの学習支援 by いっちに算数 スマホ版 「円周率と円周と直径・半径」の勉強を忘れている時は、5年の「円と正多角形」でおさらいをしまょう。 「長方形・正方形の面積」の求め方を忘れている時は、4年の「面積」でおさらいをしましょう。 この問題は、下図のように変形することができ、一辺が1cmの正方形6個分になるので、答えは 6cm 2 。 算数オリンピック(04)ファイナル 同じ中心を持ち半径の差が2cmの2つの円の内側にそれぞれ接する2つの正十二角形があります。自分で簡単に求めることができた。 アンケートにご協力頂き有り難うございました。 送信を完了しました。 正多角形の面積から辺 のアンケート記入欄 年齢 歳未満 歳代 30歳代 40歳代 50歳代 60歳以上 職業 小・中学生 高校・専門・大学生・大学



长方形和正方形面积 汇报演示 课件发布 Favorshow Com 非我秀 Powered By Discuz



如图 已知等腰三角形面积为1 求正方形面积 网易视频
第34問 内接円の面積比 図形ドリル 6年生 内接円 円 外接円 正三角形 正方形 ★★★★☆☆(中学入試難関校レベル) 思わず「お~~!!」と言いそうな良問を。受験算数の定番からマニアックな問題A:断面積(cm 2 ) e:図心からの距離(cm) I:断面二次モーメント(cm 4 ) Z:断面係数(cm 3 ) → I/e i:断面二次半径(cm) → √(I/A) 正方形 A = a 2 e = a/2 I = a 4 /12 Z = a 3 /6 i = a / √12 = 0267a 正方形 A = a 2 e = a / √2 I = a 4 /12 Z = a 3 / ( 6√2 ) i = a 正方形的面积等于边长的平方:S=a*a,也就是边长乘以边长。 已知正方形面积S,要就正方形边长,方法为 边长a²=S a=根号S 例:已知正方形面积为16,求正方形边长 a²=16 a=4 另一种正方形面积计算公式 正方形面积=对角线×对角线÷2
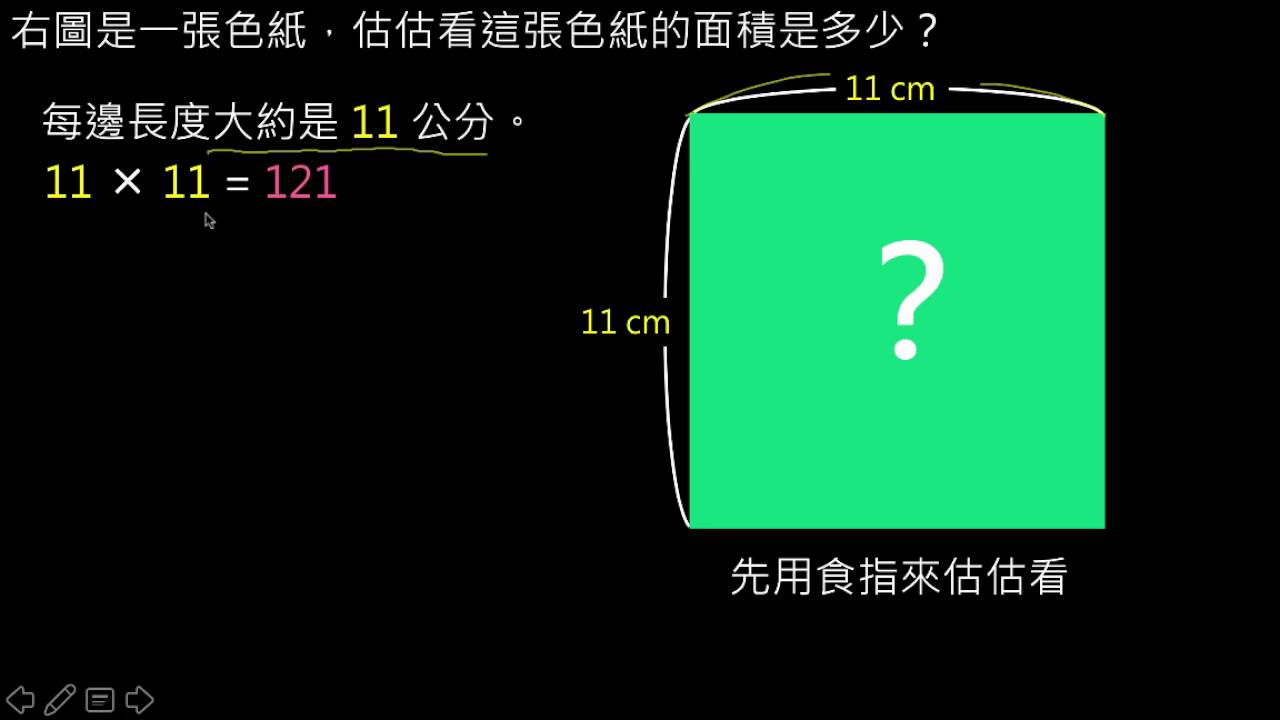



06 正方形面積公式的應用 Youtube



正方形面積 Geogebra
第131問 正方形の面積 図形ドリル 45度 6年生 正方形 直角二等辺三角形 ★★☆☆☆☆(小学4〜5年生対象) 思わず「お~~!!」と言いそうな良問を。受験算数の定番からマニアックな問題まで。図形ドリルでは,色々なタイプの図形問題を取り上げて6. 等角或补角的三角形面积的比,等于夹等角或补角的两边的乘积的比;等角的平行四边形面积比等于夹等角的两边乘积的比; 7 任何一条曲线都可以用一个函数y=f (x)来表示,那么,这条曲线所围成的面积就是对X求积分。 设圆半径为r,面积为S,则面积S=π この答えをよく見てみると、 $18\pi36$ のうち、 $36$ は正方形の面積を表していると考えられます。では $18\pi$ は何かというと、円の面積は $36\pi \mathrm{ cm }^2$ なのだから、これは半円の面積だと考えることができます。




正方形面積換算周長正方形 長方形周長與面積 Wjklv




五年級 數學 圖形的面積flashcards Quizlet
正八角形の中に二等辺三角形が8つ分できてることに気が付きますね。 なので、 二等辺三角形の面積を求めて、それを8つ分にする。 という考え方で正八角形の面積を求めていきます。 中心の360°を8等分していることから面積の計算 ・ 正三角形の面積 ・ 三角形の面積 (底辺と高さ) ・ 三角形の面積 (2辺と間の角度) ・ 三角形の面積 (1辺と両端の角度) ・ 三角形の面積 (3辺の長さ) ・ 正方形の面積 ・ 長方形の面積 ・ 台形 面積を求めたい部分(膨らんだ正方形に似た感じの図形)の上の頂点をe、右の頂点をfとする。 ステップ1: 図形aedの面積 = 正方形abcd 三角形ebc 扇形abe*2 =10^2 (1/2)*10*5√3 π*10^2*(30/360)*2 =√3(50/3)π ステップ2: 図形defの面積 = 正方形abcd 扇形abc



正方形面积求边长视频 视频在线观看 微短视频网




三下长方形和正方形面积计算练习题 Doc 文档分享网
採点する やり直す 解説 3 半径 10 ,中心角が90°の扇形の面積 円の面積の4分の1だから,10 2π ÷4=25 π π 採点する やり直す 解説 4 下の図の灰色で示した図形の面積 扇形の面積は円の4分の1で25 π ,これから三角形の面積 10×10÷2=50 を引く円の面積 円の面積は,半径×半径×314で求められます。 この求積公式の指導にあたっては,公式の理解はもとより,そこに至る過程を大切に指導することが重要です。 まず,半径10cmの円の面積が半径 (10cm)を1辺とする正方形の面積のおよそ何倍になるか解法の見通し 求める面積は左図のχの部分 つまり、正方形から a,b,c,dの4カ所を ひいてやれば良いことが分かる! a,b,c,d は合同なので a の面積だけの求め方を考える! a の部分の面積を求めるには左図の手順でよい! χ=(正方形)-(a+b+c+d)



长方形与正方形面积计算 四 面积计算 奥数网



1



三年级长方形与正方形面积练习题及答案 巧求周长 奥数网




正方形的周长公式 长方形正方形面积和周长的公式 三人行教育网 Www 3rxing Org




长方形 正方形面积的计算 Ppt 皮匠网




求正方形的面积 Youtube



正方形面积对角线公式正方形面积的对角线公式是什么 天奇生活




长方形和正方形的面积教学 图文教程 杀毒软件之家



大正方形面积 小正方形面积多24平方米 求小正方形面积 网易视频




正方形面積 Youtube



正方形面积公式推导 搜狗图片搜索



三年级数学 长 正方形的周长 面积公式 知识清单 哔哩哔哩 つロ干杯 Bilibili



长方形正方形面积的计算课件3 人教版小学数学三年级下册课件 小学课件 中国儿童资源网




孩子读三年级 一定要掌握这几种面积应用题的做法 网易订阅



技巧 数学图形面积计算的十种方法 正方形




3种方法来计算正方形的面积



三年级长方形与正方形的面积专题练习




3种方法来计算正方形的面积




3种方法来计算正方形的周长
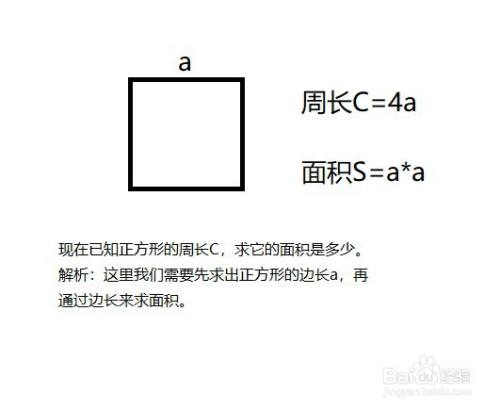



知道正方形面积怎么算周长 百度经验



三下数学第六单元长方形 正方形面积计算练习课件 沃文网wodocx Com
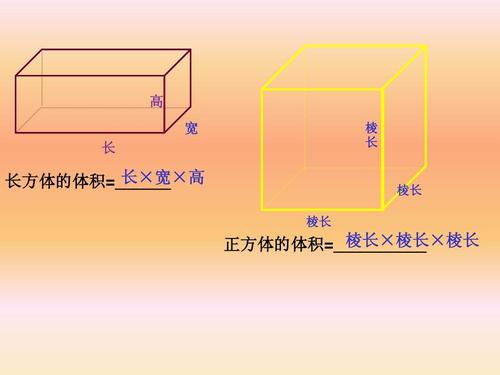



正方体面积计算公式 正方体的体积公式和正方体的表面积公式 作业帮



三年级下册数学长方形 正方形的面积应用题 附加答案 可打印 边长




周長與面積 Mathematics Quizizz



长方形 正方形面积的计算 人教版三年级下册数学电子课本 数九网
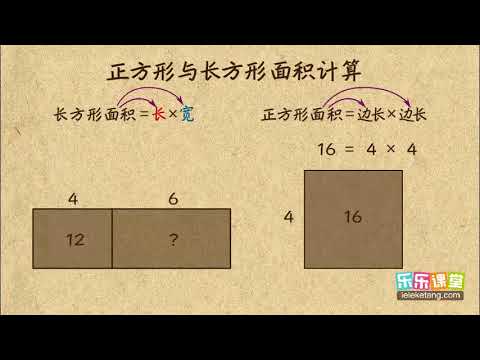



29 1 正方形 长方形面积计算小學奧數四年級幾何 Youtube



五年级数学下册 比较圆和正方形面积的一个结论的推导 长方形




正方形周长面积公式




奥林匹克训练题库 正方形与长方形 Doc 文档分享网



腾讯视频




无人不知的 面积单位 简书




正方形面积公式周长第1页 驾考预约大全



9厘米5厘米3厘米求正方形面积9厘米5厘米3厘米正方形面积是多少 答案圈
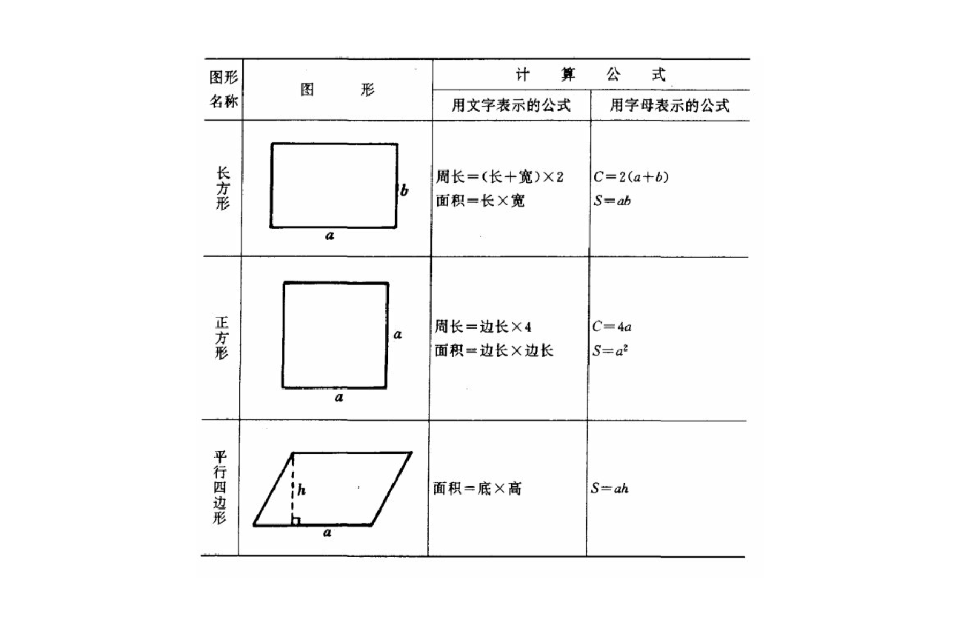



面積公式 常見面積定理 圓公式 扇形公式 圓環面積 三角形公式 海倫公式 坐標公式 中文百科全書




呈分試數學科必睇 圖形題目重點溫習攻略 公式 題目 學而思香港




如何计算正方形的周长 生活百科



正方形长方形面积公式 搜狗图片搜索



用正方形对角线如何求面积 很多学校老师不讲 但小升初常考内容 哔哩哔哩 Bilibili




05 正方形的面積公式 Youtube



正方形面积公式是什么




数单位正方形求面积计算公式 视频 长方形 正方形面积的计算 可汗学院
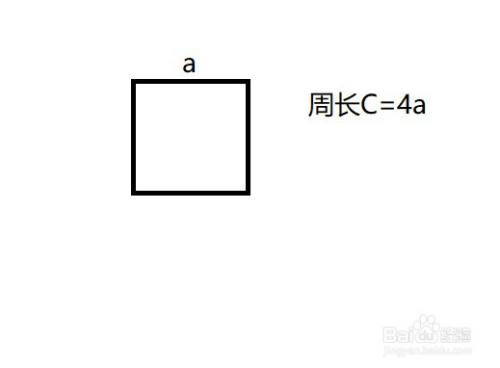



知道正方形面积怎么算周长 百度经验




长方形 正方形面积的计算 面积ppt课件下载下载 牛二ppt




正方形面积公式周长第1页 驾考预约大全



正方形面积公式 长方形和正方形面积计算 教学反思 学习岛




解没有文字说明的求正方形面积题




正方形的面积公式是什么 正方形面积算法 合抱木装修网




小升初数学必会的10种图形求面积解题法 经典收藏版 最全汇总 每日头条




正方形面积公式 正方形面积公式对角线 环球信息网




正方形面积公式周长第1页 驾考预约大全
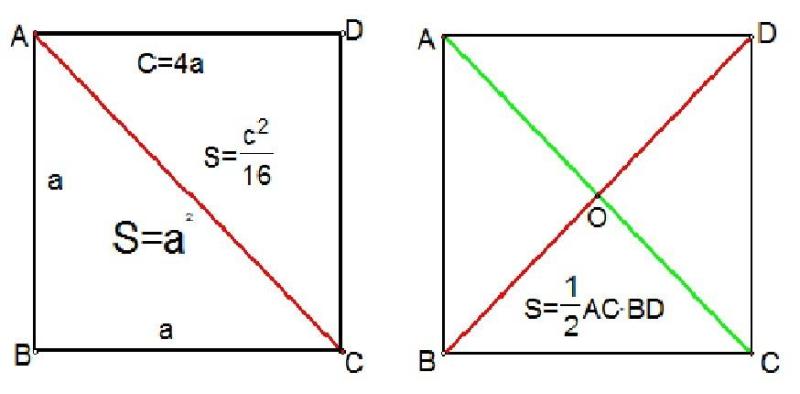



正方形面积计算公式 数学公式 搜狗百科



1



长方形和正方形面积的计算课件5 人教版小学数学三年级下册课件 小学课件 中国儿童资源网




Python中计算正方形面积的方法 视频 提高版三年级下册数学长方形和正方形面积的计算 康少妈爱康少的博客 Csdn博客



3 31长方形 正方形面积计算练习 哔哩哔哩 つロ干杯 Bilibili




正方形内最大圆的面积 在一个正方形内画一个最大的圆 这个圆的面积占正方形面积的百分之几 三人行教育网 Www 3rxing Org



三樂學院 矩形abcd被分成六個正方形 其中最小正方形面積等於1 雪花新闻




长方形和正方形的面积计算教学设计 长方形和正方形的面积计算公式是怎么来的 三人行教育网 Www 3rxing Org




正方形面积公式是什么并且有一个角是直角的平行四



长方形 正方形面积的计算 面积ppt课件 第2课时 第一ppt



正方形面积公式字母 万图壁纸网



正方形面积对角线公式正方形面积对角线的公式是什么 天奇生活



长方形 正方形面积的计算 面积ppt 第1课时 第一ppt




小學奧數 巧算長方形 正方形面積 雪花新闻



长方形 正方形面积的计算 面积ppt课件 第2课时 第一ppt




Learnmode 學習吧



面积公式 快懂百科




正方形面积计算公式 数学公式 搜狗百科



三角形面積



非常火的一道网红题 怎么求正方形面积 用对方法可以口算 哔哩哔哩 Bilibili




C 语言 正方形 圆形 利用接口实现周长及面积的计算 的技术博客 51cto博客




File 正方形内部一点到四顶点距离 与面积1 Jpg 维基百科 自由的百科全书
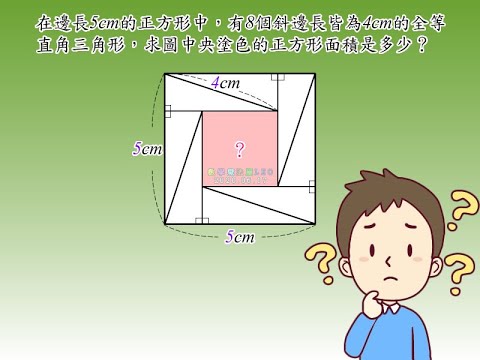



0617 正方形中的正方形面積 Youtube



長方形面積




正方形面積 Geogebra



9厘米5厘米3厘米求正方形面积怎么算 抖音求正方形面积计算方法 图 特下载



陰影面積問題 之十 雪花新闻




Mastermindlearning 小四正方形面積和周界 逆轉 與 互換 技巧 點解學校從來冇禁教 歡迎查詢聯絡 Is Gd 1vmgd2 Http Wa Me 四捨五入 設題 大量數




初二數學 3個正方形兩兩重疊 你知道怎麼求陰影部分的面積嗎 每日頭條



周长相等 正方形 长方形 圆形谁的面积较大 秦学教育



直角三角形abc 内接正方形s1 的面积为441 S2 的面积为440 求ac Cb 基础数学




三年级下册数学 长方形和正方形的面积 练习检测试卷免费下载 302edu教育资源网




基測數學 93v2 單選30 正方形 面積 評量專區 均一教育平台




大正方形面积比小正方形面积多24平方米 求小正方形面积是多少 Youtube



正方形中e是bc中点 四边形abef面积为45 求正方形面积 哔哩哔哩 Bilibili



圆面积公式计算正方形面积计算公式正方形面积的计算公式是什么 尚书坊



正方形面积对角线公式正方形面积的对角线公式是什么 天奇生活




怎樣才能算出正方形的邊長 Pisani




长方形 正方形面积的计算 面积ppt教学课件下载 牛二ppt
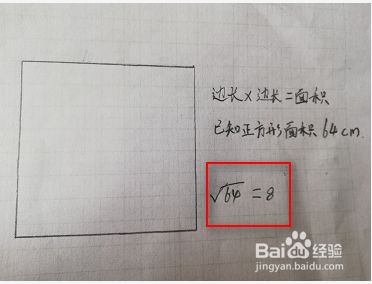



己知正方形面积求边长的方法 百度经验



0 件のコメント:
コメントを投稿