
高校数学 2元2次連立方程式3パターン 受験の月
連立方程式の解き方 この頁では,未知数の個数と方程式の個数とが等しい (*)ような連立1次方程式の解き方を扱う.さらに,係数行列に逆行列が存在する場合 (**)だけを扱う. 連立1次方程式の解き方 未知数がn個 x 1, x 2, x 3, ··, x n ,方程式がn個の連立1連立方程式では,1つの文字を「消去」して文字の個数を減らせばよい. この形の連立方程式では, (1) (2)の y の係数がそろっているところに着目すると, (1) (2)の各辺を「 引き算 」すると y を消去 できます. 例題 C2 次の連立方程式を解きなさい. 3x
連立方程式 解き方 4つ
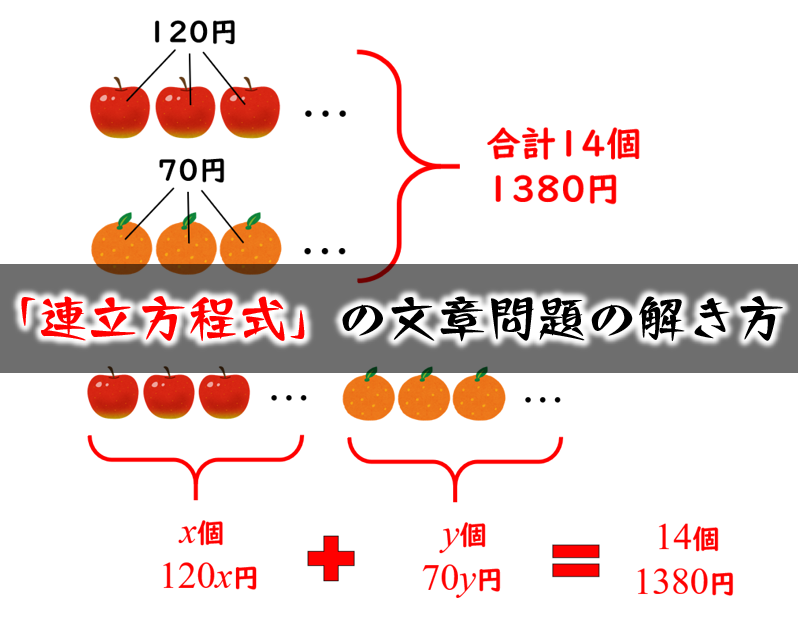
連立方程式 解き方 4つ- 連立方程式の式のつくり方、具体的に解説 (1)数と量の例題 手順1.問題文を分ける。 手順2.条件をすべて書きだす。 手順3.解りにくいならイラストや表を描いてみる。 手順4.求めるものをx(エックス)とy(ワイ)におきかえる。 手順510元連立方程式で何度値を入力しても明らかに異なる値が出力される 7 0635 歳未満 / 高校・専門・大学生・大学院生 / 少し役に立った /

式が4つ 未知数2つの連立方程式ってどうやって解けば良いのでしょうか 適当 Clearnote
4元連立方程式の解き方を教えてください。 {1}4元連立方程式を2通りの方法で解きなさい。という問題です。 ①+②+③+④から⑤を作り、⑤÷3と①、②、③を利用する方法は解けたのですが、 wのない式を3つ作る方法がわかりません。 のような連立方程式を、 解いている子です。 解けそうで、 解けない連立方程式です。 「どうやるの?」と、 この子から聞かれます。 いい聞き方です。 「分からない」ではありません。 解こうとしています。 解いて、答えを出したいのです。 でも、解き方が思い付かなくて、 解き方を教 拡大係数行列 (A, \boldsymbol{b}) を用いて,連立一次方程式を解きましょう。解き方は, 行基本変形のみを用いて, A を簡約化するように, (A, \boldsymbol{b}) を変形していきます。 「行基本変形」とは,以下の3つの変形のことを言います。
連立方程式とは、一般的に といった形で表すことが多い式です。 2元1次方程式と呼ばれる「 2つの変数 (文字) 」と「 最大次数が1 」の式で表されます。 連立方程式の解き方は大きく2つあります。 それは、 加減法 代入法 です。 どちらを用いても こんにちは、ももやまです。 今回は、前回に引き続き連立微分方程式について説明していきたいと思います。 今回は、4つの連立微分方程式の解き方 高階(2階以上)微分方程式に変換する方法 行列の対角化・ 連立方程式の未知数が4つでも、係数を見比べることで、解く前に解き方を決める子に育てることが可能です。 連立方程式 を解く前に、 未知数に付いている数(係数)を、すべて同時に見て、 どのように解くのかを決める子です。 この子の頭の中の考え
連立方程式 解き方 4つのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 | 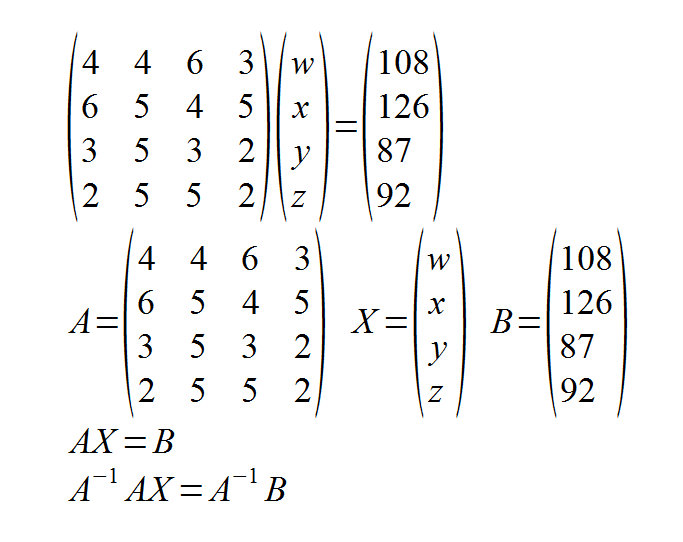 | |
 |  |  |
「連立方程式 解き方 4つ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  | |
「連立方程式 解き方 4つ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「連立方程式 解き方 4つ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「連立方程式 解き方 4つ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
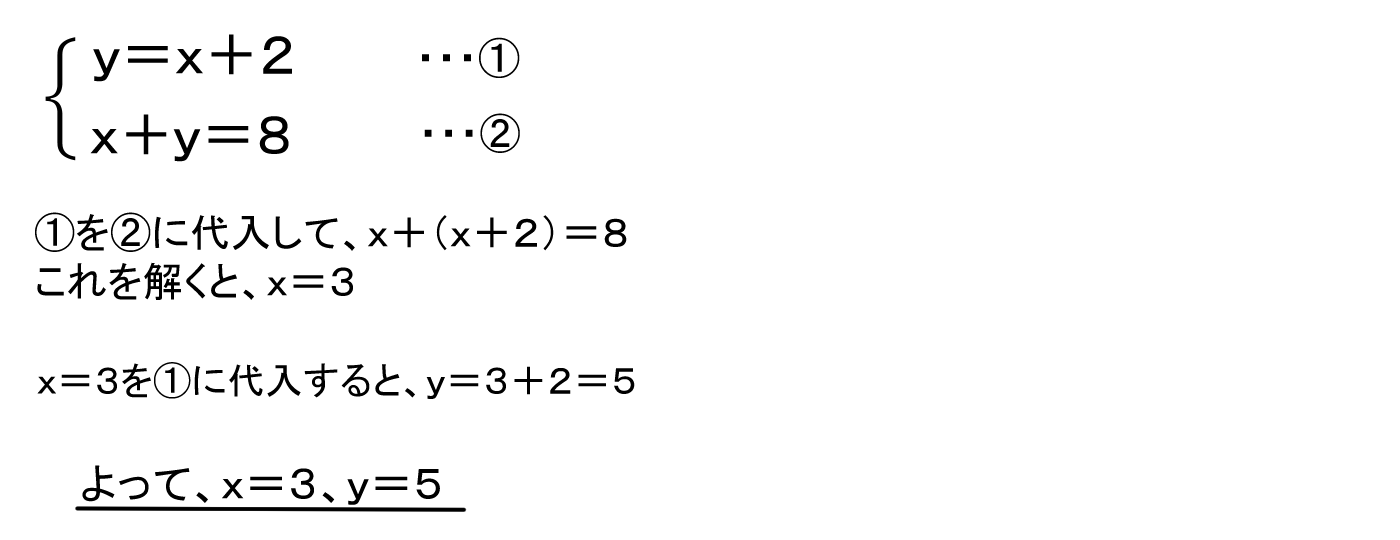 |  | |
 | ||
「連立方程式 解き方 4つ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「連立方程式 解き方 4つ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「連立方程式 解き方 4つ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「連立方程式 解き方 4つ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「連立方程式 解き方 4つ」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  | |
「連立方程式 解き方 4つ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「連立方程式 解き方 4つ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | 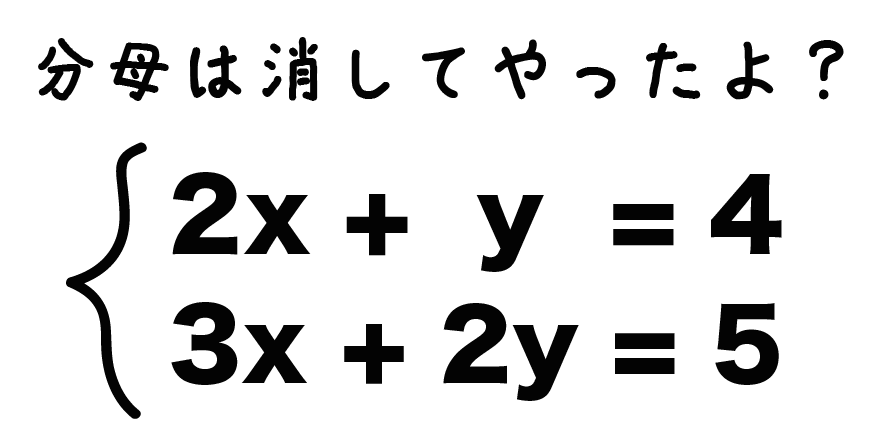 |
 |  |
その上で導いた連立方程式の解\(\boldsymbol{x_0}\)が特殊解である。 Step2 \(A\boldsymbol{x}=\boldsymbol{o}\)の任意解(全ての解)を求める 「変数の個数 – 階数」個の変数に好きな値を与え(1つだけ「1」で、残りはオール0がオススメ)、これを用いて連立方程式を解く。 連立方程式の2つの解き方(代入法と加減法) この記事では、連立方程式の2つの解き方( 代入法 と 加減法 )を紹介します。 連立方程式は、最初は戸惑うかもしれませんが、何問も繰り返して解いていくうちに当たり前のようにできるようになります。
Incoming Term: 連立方程式 解き方 4つ,




0 件のコメント:
コメントを投稿